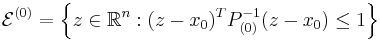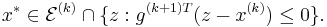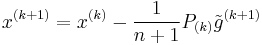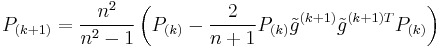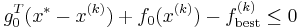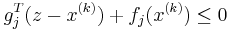Ellipsoid method
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions. When specialized to solving feasible linear optimization problems with rational data, the ellipsoid method is an algorithm, which finds an optimal solution in a finite number of steps.
The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function.
Contents |
History
The ellipsoid method has a long history. As an iterative method, a preliminary version was introduced by Naum Z. Shor. In 1972, an approximation algorithm for real convex minimization was studied by Arkadi Nemirovski and David B. Yudin (Judin). As an algorithm for solving linear programming problems with rational data, the ellipsoid algorithm was studied by Leonid Khachiyan: Khachiyan's achievement was to prove the polynomial-time solvability of linear programs.
Following Khachiyan's work, the ellipsoid method was the only algorithm for solving linear programs whose runtime was probably polynomial. However, the interior-point method and variants of the simplex algorithm are much faster than the ellipsoid method in practice. Karmarkar's algorithm is also faster in the worst case.
However, the ellipsoidal algorithm allows complexity theorists to achieve (worst-case) bounds that depend on the dimension of the problem and on the size of the data, but not on the number of rows, so it remains important in combinatorial optimization theory.[1][2][3][4]
Description
A convex minimization problem consists of a convex function 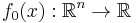 to be minimized over the variable
to be minimized over the variable  , convex inequality constraints of the form
, convex inequality constraints of the form 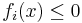 , where the functions
, where the functions 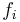 are convex, and linear equality constraints of the form
are convex, and linear equality constraints of the form 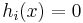 . We are also given an initial ellipsoid
. We are also given an initial ellipsoid 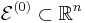 defined as
defined as
containing a minimizer 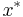 , where
, where 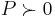 and
and 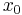 is the center of
is the center of 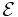 . Finally, we require the existence of a cutting-plane oracle for the function
. Finally, we require the existence of a cutting-plane oracle for the function 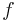 . One example of a cutting-plane is given by a subgradient
. One example of a cutting-plane is given by a subgradient 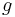 of
of 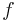 .
.
Unconstrained Minimization
At the 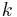 -th iteration of the algorithm, we have a point
-th iteration of the algorithm, we have a point 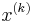 at the center of an ellipsoid
at the center of an ellipsoid 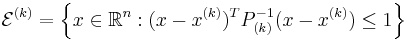 . We query the cutting-plane oracle to obtain a vector
. We query the cutting-plane oracle to obtain a vector 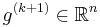 such that
such that 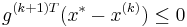 . We therefore conclude that
. We therefore conclude that
We set 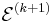 to be the ellipsoid of minimal volume containing the half-ellipsoid described above and compute
to be the ellipsoid of minimal volume containing the half-ellipsoid described above and compute 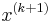 . The update is given by
. The update is given by
where 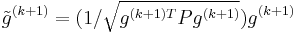 . The stopping criterion is given by the property that
. The stopping criterion is given by the property that
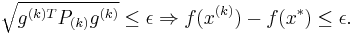
Inequality-Constrained Minimization
At the 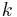 -th iteration of the algorithm for constrained minimization, we have a point
-th iteration of the algorithm for constrained minimization, we have a point 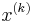 at the center of an ellipsoid
at the center of an ellipsoid 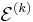 as before. We also must maintain a list of values
as before. We also must maintain a list of values 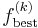 recording the smallest objective value of feasible iterates so far. Depending on whether or not the point
recording the smallest objective value of feasible iterates so far. Depending on whether or not the point 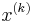 is feasible, we perform one of two tasks:
is feasible, we perform one of two tasks:
- If
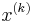 is feasible, perform essentially the same update as in the unconstrained case, by choosing a subgradient
is feasible, perform essentially the same update as in the unconstrained case, by choosing a subgradient 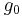 that satisfies
that satisfies
- If
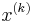 is infeasible and violates the
is infeasible and violates the  -th constraint, update the ellipsoid with a feasibility cut. Our feasibility cut may be a subgradient
-th constraint, update the ellipsoid with a feasibility cut. Our feasibility cut may be a subgradient  of
of 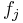 which must satisfy
which must satisfy
for all feasible 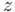 .
.
Application to Linear Programming
Performance
The ellipsoid method is used on low-dimensional problems, such as planar location problems, where it is numerically stable. On even "small"-sized problems, it suffers from numerical instability and poor performance in practice.
However, the ellipsoid method is an important theoretical technique in combinatorial optimization. In computational complexity theory, the ellipsoid algorithm is attractive because its complexity depends on the number of columns and the digital size of the coefficients, but not on the number of rows.
References
- ^ M. Grötschel, L. Lovász, A. Schrijver: Geometric Algorithms and Combinatorial Optimization, Springer, 1988.
- ^ L. Lovász: An Algorithmic Theory of Numbers, Graphs, and Convexity, CBMS-NSF Regional Conference Series in Applied Mathematics 50, SIAM, Philadelphia, Pennsylvania, 1986.
- ^ V. Chandru and M.R.Rao, Linear Programming, Chapter 31 in Algorithms and Theory of Computation Handbook, edited by M. J. Atallah, CRC Press 1999, 31-1 to 31-37.
- ^ V. Chandru and M.R.Rao, Integer Programming, Chapter 32 in Algorithms and Theory of Computation Handbook, edited by M.J.Atallah, CRC Press 1999, 32-1 to 32-45.
Bibliography
- Dmitris Alevras and Manfred W. Padberg, Linear Optimization and Extensions: Problems and Extensions, Universitext, Springer-Verlag, 2001. (Problems from Padberg with solutions.)
- V. Chandru and M.R.Rao, Linear Programming, Chapter 31 in Algorithms and Theory of Computation Handbook, edited by M.J.Atallah, CRC Press 1999, 31-1 to 31-37.
- V. Chandru and M.R.Rao, Integer Programming, Chapter 32 in Algorithms and Theory of Computation Handbook, edited by M.J.Atallah, CRC Press 1999, 32-1 to 32-45.
- George B. Dantzig and Mukund N. Thapa. 1997. Linear programming 1: Introduction. Springer-Verlag.
- George B. Dantzig and Mukund N. Thapa. 2003. Linear Programming 2: Theory and Extensions. Springer-Verlag.
- M. Grötschel, L. Lovász, A. Schrijver: Geometric Algorithms and Combinatorial Optimization, Springer, 1988
- L. Lovász: An Algorithmic Theory of Numbers, Graphs, and Convexity, CBMS-NSF Regional Conference Series in Applied Mathematics 50, SIAM, Philadelphia, Pennsylvania, 1986
- Kattta G. Murty, Linear Programming, Wiley, 1983.
- M. Padberg, Linear Optimization and Extensions, Second Edition, Springer-Verlag, 1999.
- Christos H. Papadimitriou and Kenneth Steiglitz, Combinatorial Optimization: Algorithms and Complexity, Corrected republication with a new preface, Dover.
- Alexander Schrijver, Theory of Linear and Integer Programming. John Wiley & sons, 1998, ISBN 0-471-98232-6
External links
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||